Что такое абсолютная и относительная высоты? в чем их отличие?

Содержание:

Как измеряют относительные высоты?
Разница между абсолютной и относительной высотой
Почему используют оба значения высоты
Сравнение
Впадины Земли
Почему используют оба значения высоты
Как рассчитать относительную высоту
Что такое абсолютная высота?
Почему используют оба значения высоты
Что такое высота и зачем ее используют в географии?
Что такое нулевая поверхность
Альтитуды природных ресурсов[]
Как определяется относительная высота
Примечания
Сравнение
История понятия
Смотрите так же

Как измеряют относительные высоты?

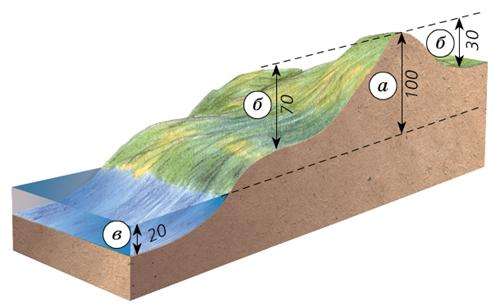
Теперь вы поняли, чем абсолютная высота отличается от относительной в географии. Для определения относительных высот удобно пользоваться специальным прибором — рейкой. Для этого в начальной точке, относительно которой ищется превышение, ставится рейка. Условно эта точка принимается за высоту с отметкой 0. Далее, как показано на рисунке выше, необходимо двигаться вверх по холму или горе до тех пор, пока вы не достигнете высоты рейки, и самая высокая ее точка не окажется ниже уровня ваших ног.

Тогда необходимо зафиксировать точку на холме, которая соответствует положению самой высокой точки рейки, стоящей на нулевом уровне, и сместить рейку в данную точку. Таким образом, на второй точке относительная высота будет равна 1 высоте рейки. Операцию нужно проделать до тех пор, пока вы не достигнете самой высокой точки холма. В этом случае относительная высота будет равняться сумме всех высот переставляемой рейки.

Вместо рейки можно использовать любой предмет, высота которого известна заранее. Если под рукой нет совсем ничего, относительную высоту можно измерить по своему собственному росту, проделав описанные выше манипуляции. Кроме того, относительную высоту легко можно измерить как разность абсолютных высот, если они заранее известны.

Разница между абсолютной и относительной высотой

С высоты воробьевых гор

Допустим, вы идете по дороге и видите перед собой возвышенность. К вам подходит добрый волшебник и говорит: «Вот тебе линейка в 6437 метров, я превращу тебя в великана, и если ты измеришь гору, то сможешь унести с собой 5 килограммов золота». Вы соглашаетесь (кто же не хочет 5 кг золота?!), начинаете расти и приставляете к горе линейку.

Итак, гора получилась 3450 метров в высоту. Но волшебнику нужно еще одно число. Значение, которое вы получили, будет называться относительной высотой. Потому что она была измерена относительно другой поверхности. Теперь вам нужно найти абсолютную высоту. Чтобы это сделать, необходимо измерить размер горы, начиная от уровня моря. Теперь в горе целых 4500 метров. Вы справились с заданием и получили свое золото.

На картах и планах указывается размер какой-либо возвышенности (горы или холма) относительно уровня моря. Относительная высота появилась гораздо раньше абсолютной. Появление второй, вероятнее всего, стало следствием развития физической географии. Именно благодаря абсолютной высоте мы знаем самую высокую и самую низкую точку нашей планеты.

Почему используют оба значения высоты

Барселона с высоты птичьего полета

Можно было бы решить, что вполне достаточно какой-то одной высоты. Но рассмотрите ситуацию, когда, например, вам нужно узнать глубину ущелья, расположенного высоко в горах. Проблема в том, что его абсолютная глубина может быть всего пару метров с учетом уровня моря, а вот относительная — составить несколько сотен метров.

Существует много интересных фактов о высотах и впадинах. Знаете ли вы, что:

глубины и впадины принято считать отрицательными формами рельефа;
если брать за основу относительную высоту, то самой высокой вершиной мира считалась бы гора Арарат;
для всего СССР была одна общая точка отсчета для АВ, и ею являлся уровень воды озера Байкал;
у горы Канченджанга разница между АВ и ОВ составляет почти 4,5 тысячи метров.

Сравнение

Что такое равнина: характеристики и виды

Таким образом, отличие абсолютной высоты от относительной заключается в том, что принимается за исходную точку. В первом случае в качестве ориентира выступает горизонтальная плоскость моря, находящегося в спокойном состоянии. Причем если объект размещен над этим уровнем, то значение абсолютной высоты является положительным, а при расположении ниже упомянутой поверхности данный показатель будет отрицательным.

Именно абсолютную высоту гор, равнинных площадей и других составляющих рельефа отмечают на планах и картах. Это обеспечивает максимальную согласованность величин. Однако уровень морей оказывается не везде одинаковым. Поэтому ученые договариваются, какую именно поверхность следует принимать за ноль.

Так, в России и близлежащих странах при измерении высоты объектов отталкиваются от уровня, соответствующего Балтийскому морю. Для удобства даже очень далеко от этих водных мест закреплены специальные знаки, на которых указаны их абсолютные координаты. Пользуясь такими опорными элементами, можно найти расстояние по вертикали от исходного уровня моря до любой требуемой точки.

Рассматривая, в чем разница между абсолютной и относительной высотой, следует остановиться и на второй из них. Здесь точка отсчета намечается произвольно. Например, можно вычислить высоту холма относительно его подножья. При этом существует вероятность, что показатели, снятые с разных сторон природного объекта, будут не совпадать

Относительная высота, показывающая расстояние между близко расположенными точками, с позиции практики часто бывает более важной характеристикой, чем абсолютная, связанная с далеким морем

Инструмент, используемый для определения высоты, – нивелир. Простейший его вариант представляет собой метровую рейку, к верху которой перпендикулярно присоединена короткая планка с отвесом. Последний компонент позволяет устанавливать нивелир строго вертикально. При измерении высоты, к примеру, того же холма приспособление размещают у его подошвы. Развернув короткую планку в сторону склона, «прицеливаются» с помощью нее, то есть мысленно проводят линию, продолжающую эту горизонталь.

Конечная точка (она оказывается на высоте одного метра от подножья) становится следующей опорой для нивелира. Все действия повторяются, а после достижения вершины объекта производятся подсчеты относительно общей высоты холма.

Впадины Земли

Самые глубокие места планеты наблюдаются в океанических глубоководных желобах. В Тихом океане находятся 3 желоба с глубиной больше 10 км: Марианский (11022 м), Тонга (10882 м), Филиппинский (10265 м). Эти глубины до последнего времени были недоступны, только с появлением специальных глубоководных батискафов это стало возможным. В 2012 году был совершен спуск в Марианскую впадину в батискафе Deepsea Challenger, где проводились фото- и видеосъемки, а также отбирались образцы грунта. До этого только батискаф «Триест» (1960 год) смог достичь дна впадины, но никаких исследований произвести не удалось.

Самая глубокая континентальная впадина – котловина Байкала (1185 м ниже уровня моря), являющаяся рифтовой зоной.

Еще одна глубочайшая впадина на материке расположена под антарктическим ледяным щитом, ее абсолютный уровень = -2555 м.

Почему используют оба значения высоты

Существует много интересных фактов о высотах и впадинах. Знаете ли вы, что:

глубины и впадины принято считать отрицательными формами рельефа;
если брать за основу относительную высоту, то самой высокой вершиной мира считалась бы гора Арарат;
для всего СССР была одна общая точка отсчета для АВ, и ею являлся уровень воды озера Байкал;
у горы Канченджанга разница между АВ и ОВ составляет почти 4,5 тысячи метров.

Как рассчитать относительную высоту

Для начала надо выбрать точку, от которой будет вестись отсчет. Для гор такой точкой выбирают основание. Если определяют относительные высоты нескольких горных вершин, точкой отсчета является соединяющая их седловина.

Седловина, кстати, действительно разделяет горы так, что напоминает седло.

Если гора печальна и одинока, ее относительную высоту часто считают равной абсолютной.

И абсолютные, и относительные высоты имеют большое значение для описания рельефа. Относительная высота — важный критерий, по которому определяют, является гора самостоятельной вершиной или частью, т.е. пиком, другой.

Относительную высоту могут рассчитывать не только географы, но и все желающие. Например, ничто не мешает мне вычислить свою высоту относительно моей кошки.

И наконец раскрою интригу. Кто самый-самый по относительной высоте? Зависит, от чего отсчитывать. Если от основания, то высота гавайской Мауна-Кеа составит более 10 километров (это выше Эвереста, чтоб вы знали). Вот только большая часть основания у нее ниже уровня моря.

Что такое абсолютная высота?

Абсолютная высота — расстояние между какой-либо точкой и среднемноголетним показателем уровня океана или моря. В России, Польше и большинстве стран СССР за этот показатель принят среднемноголетний уровень Балтийского моря. Для других частей света отметка расположена в других местах. Относительно уровня моря измеряют как высоту географических объектов, так и их глубину. Таким образом, этот показатель может быть положительным и отрицательным. Абсолютную высоту также называют альтитудой, а обозначают как н.у.м, например, 2228 м н.у.м (г. Косцюшко). Этот показатель дополняет широту и долготу — две основных координаты точки. Измеряют абсолютную высоту путем нивелирования.

Почему используют оба значения высоты

Существует много интересных фактов о высотах и впадинах. Знаете ли вы, что:

глубины и впадины принято считать отрицательными формами рельефа;
если брать за основу относительную высоту, то самой высокой вершиной мира считалась бы гора Арарат;
для всего СССР была одна общая точка отсчета для АВ, и ею являлся уровень воды озера Байкал;
у горы Канченджанга разница между АВ и ОВ составляет почти 4,5 тысячи метров.

Что такое высота и зачем ее используют в географии?

Вам будет интересно:ЛАИ — это экономический или политический союз?

Любой географический объект, расположенный на поверхности Земли, обладает определенным набором координат (широта и долгота), а также высотными характеристиками. Рельеф нашей планеты неоднороден, где-то доминируют высокие горы, где-то глубоко вниз уходят бездонные впадины и ущелья. Понятие высоты было придумано людьми, чтобы максимально точно описать те или иные особенности рельефа земной поверхности.

Кроме того, понятие высоты используется на топографических и высотных картах. Подписанная высота позволяет отобразить на плоской поверхности карты объемный рельеф. Как правило, все высоты измеряются в метрах — стандартизированной единице из международной системы. Высоты могут принимать как положительные, так и отрицательные значения. На земной поверхности диапазон высот колеблется от -400 метров (впадина Мертвого моря) до 8848 метров (высочайшая вершина мира — гора Эверест). Для того чтобы лучше понять, чем отличаются высоты, необходимо ввести понятие абсолютная и относительная высота.

Что такое нулевая поверхность

Любые объекты на карте имеют особую отметку высоты – «над» или «ниже» уровня моря. Что это за точка и как она определяется?

Уровень моря – это средняя величина, вычисляемая из уровней всех водоемов Мирового океана, находящихся в спокойном состоянии.

Измерения проводятся при помощи специальных приборов, отмечающих уровень воды по отношению к отвесной линии.

Поскольку уровень мирового океана зависит от многих факторов, то для определения среднего значения необходимо сверять данные на протяжении многих лет.

Учеными выделено несколько уровней: прилив, отлив, среднесуточный, среднегодовой и т.д. После чего, на основе многолетних исследований вычисляется среднемноголетний уровень мирового океана, который и принимается за начальную точку отсчета при измерении высот.

Опираясь на заключения специалистов, на картах и планах ставятся пометки «выше» или «ниже» уровня моря.

Из этого следует, что определение размещения объекта в пространстве по отношению к уровню моря является разницей между нулевой координатой и конечной точкой измерения.

Альтитуды природных ресурсов[]

Распределение руд до 1.18

Ниже представлена таблица, в которую занесены некоторые альтитуды и ресурсы, которые могут быть найдены в них:

Особенности ландшафта	Основная альтитуда нахождения	Чаще всего встречаются…	Редко встречаются…	Не встречаются выше…	Не встречаются ниже…	Инструменты, необходимые для получения
Угольная руда	От 0 до 264	Слой 144	От 0 до 32	Слой 270	Слой 0	Деревянная кирка или лучше
Гравий	От -64 до 192	Слой 61	От 128 до 192	Слой 192	Слой -8	Любые
Земля	От 1 до 160	Слой 64	От 128 до 160	Слой 160	Слой -8	Любые
Песок	От 28 до 120	Слой 63	От 108 до 120	Слой 120	Слой 27	Любые
Уровень моря	Слой 64	Слой 64	—	—	—	Ведро
Железная руда	От -64 до 80; От 127 до 255	Слой 32, 240	Ниже -24; Выше 56	Слой 257	Слой −64	Каменная кирка или лучше
Золотая руда	От -64 до 32	Слой −16	Ниже -48; Выше 16	Слой 32	Слой −64	Железная кирка или лучше
Медная руда	От 0 до 96	Слой 48	Ниже 16; Выше 80	Слой 96	Слой 0	Каменная кирка или лучше
Лазуритовая руда	От -64 до 64	Слой 0	Ниже -16; Выше 16	Слой 64	Слой −33	Каменная кирка или лучше
Лава	От -64 до 180	Слой -54	От 0 до 180	—	—	Ведро
Алмазная руда	От -64 до 16	Слой -60	От 0 до 16	Слой 16	Слой −64	Железная кирка или лучше
Красная руда	От -64 до 16	Слой -60	Слой −28-16	Слой 16	Слой −64	Железная кирка или лучше
Коренная порода	От -64 до -60	Слой −64	Слой -61, -60	Слой −59	Слой −64	—
Изумрудная руда	От 32 до 255	Выше 220	Ниже 108	Слой 256	Слой 32	Железная кирка или лучше

Некоторые природные ресурсы могут быть найдены в разных альтитудах, поскольку они не имеют ограничений по высоте, на которой они могут появляться в игре. Чтобы эти объекты появились в игровом мире, требуется создание условий, пригодных для их размещения.

Объект	Условия
Дёрн	Земля, свет и дёрн по соседству
Сахарный тростник	Земля или Песок, вода по соседству
Дерево	Земля, свет и пространство
Кактус	Песок, отсутствие блоков по соседству
Цветы	Земля и свет
Грибы	Сухая поверхность и темнота
Глина	Песок
Обсидиан	Лава (источник) и вода
Булыжник	Вода и лава (течение) или сокровищница
Замшелый булыжник	Сокровищница, Храм в джунглях

Как определяется относительная высота

Для определения относительной высоты используется специальная линейка – нивелир, представляющий собой рейку, высотой 1метр. К ее верхней части под прямым углом прикреплена короткая планка, которая позволяет установить рейку перпендикулярно измеряемого объекта.

Для измерения высоты нивелир устанавливается в начальной точке, принимаемой за нулевую отметку, и, развернув планку в сторону объекта измерения для проведения визуальной линии – горизонтального продолжения планки. Верхняя точка отрезка является следующей отправной точкой измерения. Таким образом, действия нужно повторять до достижения вершины измеряемого объекта. Путем сложения количества высот переставляемого нивелира вычисляется общая высота объекта.

При отсутствии специальной линейки можно воспользоваться любым другим предметом с известной высотой. Кроме того, измерить относительную высоту можно даже при помощи собственного роста.

Примечания

Болотов А. П. Геодезия или руководство к исследованию общего вида Земли, построению карт и производству тригонометрической и топографической съемок и нивелировок. Часть II: проекции карт, нивелирование, топография.. — СПб.: К. Вингебер, 1837. — 445 с.
Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 1. — Paris: Courcier, 1807. — С. 230.
Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 2. — Paris: Courcier, 1819. — С. 350.
Puissant L. Traité de topographie, d’arpentage et de nivellement. — Paris: Courcier, 1807. — 332 с.
Laplace Pierre-Simon. Traité de Mécanique céleste, t. 4. — 1. — Paris: L’Imprimerie Royale, 1805.
Wand Th. Die Principien der mathematischen Physik und Potentialtheorie. — Leipzig: B. G. Teubner, 1871. — 184 с.
Молоденский М. С. Основные вопросы геодезической гравиметрии. — Труды ЦНИИГАиК, вып. 42. — Москва: Геодезиздат, 1945. — 108 с.
Еремеев В. Ф., Юркина М. И. Теория высот в гравитационном поле Земли. — Труды ЦНИИГАиК, вып. 191. — Москва: Недра, 1972. — 144 с.

Сравнение

История понятия

К середине XIX в. стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов , следуя французскому академику отметил возможность счета высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. в книге 1805 г. описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г. Лаплас дал описание астрономической и земной рефракции и измерение высоты барометром.

Внимание геодезистов к этому кругу вопросов привлекла в 1870 г. невязка в ~1,2 м полигона геометрического нивелирования, пересекшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра

Теодор Ванд , Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности

Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд , Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

В 1945 г. М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля . Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г.

Смотрите так же

Отвесная линия — Прямая, совпадающая с направлением действия силы тяжести в данной точке.

Ориентир — Хорошо видимый на местности неподвижный предмет (естественный или искусственный) или элемент рельефа, помогающий ориентироваться на местности, определять направление при движении.

Ортотрансформирование (ортокоррекция) изображения (снимка) — Математически строгое преобразование исходного изображения (снимка) в ортогональную проекцию и устранение искажений, вызванных рельефом, условиями съемки и типом камеры.

Ортомозаика — Процесс яркостного выравнивания и объединения («сшивки») нескольких ортотранс-формированных изображений (снимков) в одно непрерывное изображение (снимок) с заранее заданным изобразительным качеством.

Опорная межевая сеть — Геодезическая сеть специального назначения (ГССН), которая создается для геодезического обеспечения государственного земельного кадастра, мониторинга земель, землеустройства и других мероприятий по управлению земельным фондом страны.

Общеземной эллипсоид — Эллипсоид, наилучшим образом согласующийся с поверхностью геоида в целом.

Общегеографические карты — Отображают с одинаковой подробностью основные природные и социально-экономические объекты (рельеф, растительность, гидрографию, населенные пункты, границы и др.). К крупномасштабным общегеографическим картам относятся топографические карты.

Ординар — Нуль футштока на водомерных постах, фиксирующий средний многолетний уровень воды в водоемах. Колебания уровня отсчитываются выше и ниже ординара с точностью до 1 см.

Основная уровенная поверхность — Поверхность, которая в каждой своей точке перпендикулярна к направлению отвесной линии и имеет постоянный потенциал силы тяжести.

Опорная геодезическая сеть — Система закрепленных на местности точек, плановое положение и высота которых определены в единой системе координат на основании геодезических измерений; эти точки служат опорными пунктами при геодезических и топографических съемках.

Ориентирование линий — Определение их направлений относительно других линий.

Обратная геодезическая задача — Заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.

Ошибок теория — Раздел математической статистики, посвященный построению уточненных выводов о численных значениях приближенно измеренных величин, а также об ошибках (погрешностях) измерений.